نظریه گراف
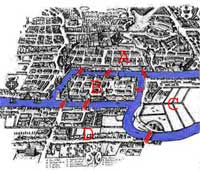
| در ریاضی و علوم کامپیوتر، نظریه گرافعلمی است که به مطالعه گرافها میپردازد.گراف مجموعهای از راسهاست که بوسیله یالها به هم وصل شدهاند.به عبارت سادهتر به مجموعهای از نقاط که بوسیله خطوط به هم وصل شدهاند، گراف گویند. مفهوم گراف در سال 1736 توسط اویلر و با طرح راهحلی برای مساله پل konigsberg ارائه شد و به تدریج توسعه یافت.گرافها امروزه کاربرد زیادی در علوم دارند. از گرافها در شبکهها،طراحی مدارهای الکتریکی, اصلاح هندسی خیابانها برای حل مشکل ترافیک،و.... استفاده میشود |
تعریف
فرض کنید V یک مجموعه ناتهی و E زیرمجموعهای از باشد در این صورت زوج
باشد در این صورت زوج 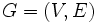 را یک گراف می نامند.V را مجموعه راس ها و E را مجموعه یال ها می گویند.
اگر ترتیب قرار گرفتن راس ها در مجموعه E مهم باشد،گراف را گراف جهتدار می گویند و یال از راس
را یک گراف می نامند.V را مجموعه راس ها و E را مجموعه یال ها می گویند.
اگر ترتیب قرار گرفتن راس ها در مجموعه E مهم باشد،گراف را گراف جهتدار می گویند و یال از راس 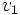 به سمت راس
به سمت راس 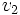 را به صورت
را به صورت 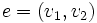 نشان میدهند.در غیر این صورت گراف را بدون جهت مینامند و یال بین راس های
نشان میدهند.در غیر این صورت گراف را بدون جهت مینامند و یال بین راس های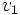 و
و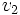 با نماد
با نماد 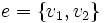 نشان میدهند.
نشان میدهند.
|
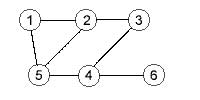
تعداد راس های یک گراف را مرتبه و تعداد یال های آن را اندازه گراف می نامیم.
در شکل روبرو گرافی را با شش راس و هفت یال مشاهده می کنیم
- گراف همبند
- گراف ناهمبند
- گراف اویلری
- گراف همیلتونی
- گراف درختی
- گراف مسطح
- گراف چندبخشی
- گراف k-مکعب
- گراف ستارهای
- گراف اشتراکی
- گراف منظم
- گراف جهتدار
گرافها و ساختار دادهها
هر گراف را میتوان با یک ماتریس نمایش داد ، که به آن ماتریسمجاورت گراف گویند. در این روش از آرایه هااستفاده میکنیم.این ماتریس به تعداد راسهای گراف دارای سطر و ستون است.وعدد 1 نشان دهنده وجود یک یال بین دو راس و عدد 0 نشان دهنده عدم وجود ارتباط بین دو راس است.یعنی ماتریس ما شامل دو عدد صفر و یک است. با استفاده از این ماتریس میتوان رئوسی را که با یک راس در ارتباطاند و نیز رئوسی را که با هیچ راس دیگری ارتباط ندارند رامشخص کرد.- تئوری رنگ آمیزی
- قضیه چهار رنگ
- مسائل حل نشده در رنگ آمیزی
- مسائل موجود در زمینه مسیر
- Minimum spanning tree
+ نوشته شده در شنبه نوزدهم مرداد ۱۳۸۷ ساعت 15:54 توسط Amir-Yeganeh
|