شگفتی ها و زیبایی های ریاضی
بسیاری از واژه ها ، عبارات و جملات وجود دارند که اگر آن ها را از ابتدا به انتها بخوانیم و یا از انتها به ابتدا بخوانیم ، یکسان اند. به این گونه واژها ، عبارات و جملات ؛ واژها ، عبارات و جملات ِ خود برعکس یا متقارن می گوییم.
به واژه ها و عبارت زیر توجه کنید :
کمک
کتک
شوش
توت
داماد
شاباش
شکربترازوی وزارت برکش
به واژگان انگلیسی زیر نیز توجه کنید :
RADAR
ROTATOR
MADAM I'M ADAM
NO LEMONS, NO MELON
در تاریخ ها نیز ، روز هایی وجود دارند که خود برعکس اند ، مثلا ً بیست و یکم خرداد ِ 1230 : 
یا بیست و یکم بهمن 1211 : 
حتی می توانیم ساعات را در این زیبایی شریک کنیم ، مثلا ً ساعت ِ نه و سی و سه دقیقه و دوازده ثانیه ی شب : 
، یا ساعت پنج و پنجاه ثانیه ی صبح : 
یا حتی یک روز مشخص از سال ، زمان مشخصی مثلا ً روز یازدهم مرداد 1363 ، ساعت پانزده و سی و شش دقیقه و سی و یک ثانیه : 
و اگر ماه ها را نیز دو رقمی بنویسیم ، تاریخ زیر خود برعکس است : 
شما نیز می توانید چنین روزهایی را بیابید ، شاید روز تولد شما چنین روزی باشد !!!
اکنون به اعداد خود برعکس می پردازیم :
به چهار توان ِ اول ِ عدد 11 توجه کنید :

یک عدد خودبرعکس می تواند عددی اول یا مرکب باشد. مثلا ً 151 یک عدد ِ اول ِ خودبرعکس است و 171 یک عدد مرکب خودبرعکس است ولی نکته جالب توجه این است که به جز عدد ِ 11 ، دیگر اعداد اول خودبرعکس ، تعداد ارقام فرد دارند.
چگونه می توان یک عدد خودبرعکس ساخت ؟
این کار بسیار ساده است و از هر عددی می توان عدد ِ خودبرعکس ساخت. عدد دلخواهی را انتخاب کنید و آن را با برعکسش جمع کنید. اگر حاصل جمع، عددی خودبرعکس بود کار تمام است وگرنه حاصل را نیز با برعکسش جمع کنید. با ادامه ی این روند ، سرانجام به عدد خودبرعکس خواهید رسید. بعضی اعداد خودبرعکس پس از یک مرحله به دست می آیند و برخی بیشتر. برای نمونه اگر عدد 23 را انتخاب کنیم پس از یک مرحله ، عدد خود برعکس به دست می آید : 23 + 32 = 55 .
با انتخاب عدد 75 ، پس از دو مرحله به عدد خودبرعکس می رسیم :

و با انتخاب 86 ، پس از 3 مرحله به عدد خودبرعکس می رسیم :

اگر 97 را انتخاب کنیم ، در 6 مرحله به عدد خودبرعکس می رسیم و برای عدد 98 ، 24 مرحله تا رسیدن فاصله است. اگر عدد 196 را انتخاب کنید ، با صبر و حوصله سرانجام به عدد خودبرعکس می رسید !!!!



















































































 را
را 









 .
.
 .
.





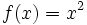

 یک تابع از f است که دارای سه پارامتر x,y,z است که یک ارزش را برای تابع تولید می کنند. از توابع چند متغیره می توان به قانون
یک تابع از f است که دارای سه پارامتر x,y,z است که یک ارزش را برای تابع تولید می کنند. از توابع چند متغیره می توان به قانون 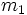 و
و 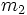 و نیز یک متغیر برای فاصله هر جرم به نام
و نیز یک متغیر برای فاصله هر جرم به نام 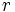 در آن وجود دارد.
در آن وجود دارد. 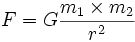

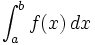 نشان می دهند علامت
نشان می دهند علامت 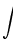 ،انتگرال گیری از تابع f را نشان می دهند ،aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال پذیر است و dx نمادی برای متغیر انتگرال گیری است.
،انتگرال گیری از تابع f را نشان می دهند ،aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال پذیر است و dx نمادی برای متغیر انتگرال گیری است. 
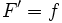
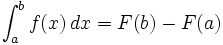
 خواهد بود.
خواهد بود. 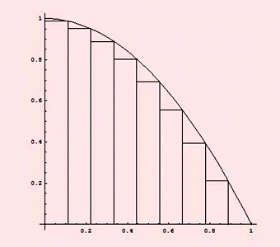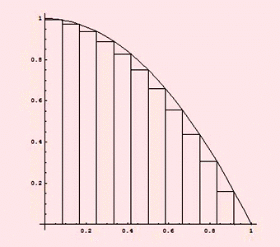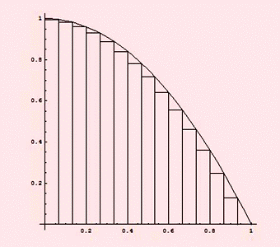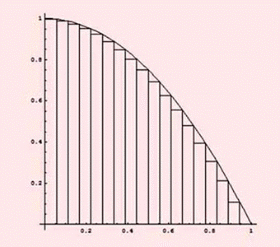





















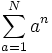

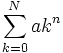
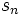 نشان میدهند
نشان میدهند 
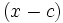 میگویند.واضح است که جملات آن به فرم زیردر میآید:
میگویند.واضح است که جملات آن به فرم زیردر میآید: 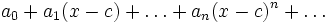
 را میتوان به صورت جمع توابعی بر حسب
را میتوان به صورت جمع توابعی بر حسب  نوشت.
نوشت. 


 .
. 
















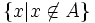
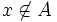 انگاه
انگاه 
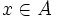 انگاه
انگاه 





